¿Cuánto tiempo esperando un eclipse total?

 

Cuando se habla del eclipse suele mencionarse cuánto hace que se produjo el anterior, o cuándo será el siguiente. Por toda la península se oye mucho eso de “hace más de 100 años”, pero en mi localidad (en Bilbao que tenemos fama de fanfarrones y exagerados) son bastantes más. Pero hay lugares que de alguna manera están gafados y parece que nunca les toca.

En cualquier caso, en algunas de las charlas que he dado al respecto o comentándolo con algún grupo casi siempre hay alguien que dice recordar que vio un eclipse total en esa misma ciudad. Que oscureció y se hizo de noche en pleno día. Hay muchos recuerdos falsos o referidos a eclipses anulares o parciales en que algo oscureció aunque no fuese mucho, pero yo le suelo decir “Pues te has cuidado muy bien y no tienes aspecto de haber cumplido ya 166 años”

Aunque en Bilbao fueron 166, en la península hace 114 años que se produjo el último, por lo que nadie ha visto desde aquí ningún otro. Habría tenido que viajar lejos para haberlo visto.

En el próximo mes de agosto desde 23 capitales de provincia podrá verse el eclipse total: A Coruña, Lugo, Oviedo, León, Zamora, Valladolid, Palencia, Segovia, Burgos, Soria, Santander, Bilbao, Vitoria-Gasteiz, Logroño, Guadalajara, Cuenca, Zaragoza, Teruel, Lleida, Tarragona, València, Castellón y Palma de Mallorca.

Al año siguiente en otras 3: Cádiz, Málaga y Almería. A modo de curiosidad, vamos a averiguar cuántos años habría que haber esperado en cada una de esas 26 ciudades para que ocurriera de nuevo un eclipse total.

Redondeadas en rojo las capitales desde las que se verá el eclipse total de 2026 o el de 2027. Curiosamente la línea de sombra en 2026 pasa cerca de Madrid y Barcelona pero no llega a tocarlas

Para ello, iremos retrocediendo en el tiempo y fijándonos en las zonas en que se vio cada eclipse.

Aunque sea por simple curiosidad, puede ser interesante…y de paso haremos referencia a los últimos eclipses totales ocurridos en la península.

- El anterior a este de 2026 ocurrió el 17 de abril de 1912. Efectivamente, parece sorprendente que hayan pasado más de 100 años mientras que entre éste y el siguiente sea poco menos de un año. En aquel caso la zona de sombra no incluyó a ninguna capital (aunque pasó cerca de Oviedo), en parte porque fue una línea muy estrecha por tratarse de un eclipse híbrido (ver el anexo)

Solo algunas zonas de las provincias de Orense, León y Asturias fueron afectadas por aquel y por éste, con lo que puede decirse que allí “solo” hay que retroceder 114 años para encontrar nuevamente el fenómeno. Y que en nuestras 26 capitales, aunque se diga lo de los 100 años, fueron más que ese tiempo.

Sí estuvo a punto de eclipsar Oporto, donde el porcentaje de Sol eclipsado fue del 99.3%

- Antes de aquel hubo otro, el 30 de agosto de 1905. Este sí con una amplia zona de sombra, extraordinariamente parecida a la de 2026, pero algo más estrecha y contenida en ella, con lo que de las actuales ciudades dejó fuera a Zamora, Segovia, Guadalajara, Cuenca, Valencia, Santander, Bilbao, Lleida, Tarragona, y por muy poco a Vitoria. Por supuesto también Cádiz, Málaga y Almería. Desde el resto de las actuales puede decirse que el anterior fue hace 121 años.

El de 1905, que fue el "anterior" a muchas de las capitales que vivirán ahora el eclipse total

- Retrocediendo más en el tiempo llegamos a 1900, concretamente el 28 de mayo, hace ya 126 años, cuando curiosamente la franja de sombra no tocó a la de 2026 ni a la 2027 y por ello no afecta a nuestro estudio, aunque sí incluyó a Oporto, Toledo, Albacete y Alicante, donde podrían tomar este dato para averiguar cuantos años deben pasar hasta el siguiente en un futuro.

El de 1900, un eclipse que no fue "el anterior" de ninguna capital actual 

- El anterior, el 22 de diciembre de 1870

En cierta manera parecido al de 2027, que tocará a Cádiz y Málaga (que así quedarán con un intervalo de 157 años) Pero no a Almería que debería ir buscando más atrás.

Huelva y Sevilla tuvieron entonces su último eclipse.

El eclipse de 1870, cuyo recorrido en la zona peninsular se parece algo al del 2027

Nos quedan por tanto Zamora, Segovia, Guadalajara, Cuenca, Valencia, Santander, Bilbao, Lleida, Tarragona, Vitoria y Almería que todavía no hemos encontrado su anterior eclipse.

- El 18-7-1860 hubo otro,  parecido también al de 2026

En aquella ocasión sí se vio el eclipse desde Valencia, Santander, Bilbao, y Vitoria, 166 años antes que el de ahora, y quedan sin encontrar el anterior Zamora, Segovia, Guadalajara, Cuenca, Lleida, Tarragona y Almería.

- El 8-7-1842 el eclipse total proyectó su sombra (entre otras ciudades) sobre Cuenca, Guadalajara, Lleida y Tarragona, que han tenido que esperar 184 años hasta el de 2026.

Por lo tanto, de las ciudades que estos dos años (2026 y 2027) serán eclipsadas, para buscar el anterior eclipse solo nos faltan Zamora, Segovia, y Almería. Que tendrían que retroceder mucho más en el tiempo porque el anterior eclipse total sobre la península fue el 26-10-1753 (un eclipse híbrido que a pesar de la estrechez de su banda oscureció Alicante, Albacete y Toledo) y antes el 12-5-1706 ¡Casi nada!

Por cierto, el eclipse de 1842 pasó por Madrid, por Barcelona, y prácticamente también por Lisboa con un 99.5% de ocultación. De los eclipses estudiados (de los últimos 200 años) este fue el único que tocó a las 3 grandes ciudades de la península.

Las 3 capitales que nos han quedado (Zamora, Segovia, y Almería) son las que verán ahora un eclipse y no tienen un precedente cercano, pero más desafortunadas son las que ni ahora, ni en estos últimos 200 años han sido testigos del extraordinario espectáculo, que las vemos superponiendo las trayectorias de los diferentes eclipses.

Trayectorias sobre la península de la sombra de los eclipses totales de los dos últimos siglos, incluidos los de 2026 y 2027

Se han quedado sin eclipse Córdoba, Jaén, Murcia, Pontevedra, Ávila, Salamanca, San Sebastián, Pamplona y Huesca, estas dos últimas por muy poco y Granada (que lo vio el 12-5-1706).

En un próximo post espero recoger  explicaciones, comentarios, detalles y definiciones que completen  de una manera más didáctica lo relatado aquí, que más que nada ha respondido a determinadas curiosidades.

La Luna adelgaza para visitar a los planetas

Los días 13,14,15, 19 y 20 de este mes de mayo podremos ver bonitas estampas en el cielo con la Luna acompañando a los planetas.

Como alguna vez he comentado, la Luna vista desde aquí sigue casi el mismo camino que los planetas (cerca de la línea de la eclíptica), pero se mueve mucho más rápido y a cualquiera de ellos le hará una visita aproximadamente cada mes.

Cuando varios de estos planetas se encuentran en una misma zona lógicamente les visitará casi a la vez y en una fase casi igual pero todo será distinto si cada uno está en una zona de cielo diferente.

Este mes de mayo de 2026 la situación puede considerarse especial, o al menos curiosa. Todos los planetas están relativamente cerca del Sol (máximo de 55 grados en distancia angular) pero los dos más brillantes (Venus y Júpiter) se ven al atardecer porque se ponen después que el Sol, mientras que otros tres (Marte, Saturno y Neptuno) salen antes que el Sol y serán visibles de madrugada (Para ver a Neptuno se necesitarán medios ópticos). 

 Por un lado la dirección de Neptuno y por otro la de Júpiter (líneas azules), delimitan dos ángulos casi iguales respecto a la dirección del Sol (línea amarilla)
Posiciones del 16-5-26. Datos tomados de Heavens-Above.

La mayor separación angular desde el Sol tanto por el Este (Júpiter) como por el Oeste (Neptuno) en estos días son casi iguales (como se ve y se indica en el gráfico), de manera que cuando la Luna se acerque a los diferentes planetas bien por la mañana, bien por la tarde, tendrá fases muy parecidas (pero inversas decreciente-creciente)

Además como estos ángulos son relativamente pequeños (podrían llegar como máximo a 180 grados el caso de la oposición) veremos a la Luna cerca de los planetas en fase muy fina (y de ahí el título del post). Estará menguante (adelgazando) cuando pase cerca de Neptuno, Saturno y Marte los días 13, 14 y 15 como se representa en el gráfico.

Latitud 43º N, una hora antes de la salida del Sol

Y  luego creciente para poder verse cerca de Venus y Júpiter el 19 y 20 al principio de la noche, pero no le dará tiempo a aumentar mucho la fase antes de despedirse de los planetas hasta el próximo mes. 

Latitud 43º N, una hora después de la puesta de Sol
Se han añadido 3 estrellas brillantes que están en la zona para una mejor localización

Por cierto, a mediados de junio habrá varias situaciones muy llamativas, que espero contaros.

Pero nos quedan 2 planetas que aún no he citado: Mercurio y Urano, que aunque también serán visitados por la Luna no podremos verlo porque es justamente el día 16, cuando estará en fase nueva (más delgada imposible) y por ello se situará angularmente muy cerca del Sol y estará por encima del horizonte de día. 

Solo como ejemplo de las posiciones, ésta sería la situación desde Aberdeen al Oeste de Canadá 15 minutos después de la puesta de Sol. Evidentemente su observación es imposible a esa hora, y luego enseguida se ponen.

Es una pena porque si pudiésemos eliminar el Sol, también veríamos una nueva ocultación de las Pléyades, una de las mejores.

Con medios sofisticados se podría ver esa ocultación desde zonas del Oeste de Norteamérica donde la Luna se pone unos 30 o 45 minutos después del Sol y en ese tiempo se produce la ocultación. Aunque nada fácil de visualizar, sería muy especial ir viendo a través de un telescopio cómo se van apagando las estrellas de las Pléyades, ocultadas por algo que no se ve (la Luna nueva), y luego aparecen misteriosamente, como en esta simulación.

Preguntas sobre el eclipse

¿Quieres preguntar algo sobre el eclipse?

Un post diferente, con una utilidad concreta:

No cabe duda de que el eclipse es el tema de actualidad en lo que a la astronomía se refiere. Yo llevo casi un maratón de charlas, que me han solicitado aquí y allá, y en la mayoría de los casos ha surgido el problema de que si hay fijada una hora de finalización (¡que tenemos que dejar libre ya el local!) hay preguntas del público que quedan sin contestar. 

Intento hacerlo luego por los pasillos o dando mi dirección de correo a mi interlocutor, pero se me ha ocurrido que va a ser mucho más fácil dar la dirección de este blog (es mucho más fácil de recordar) y que me hagan un comentario (preferentemente en este post), que yo iré actualizando con las respuestas (si están en mi mano) para todo el que le interese.

O, por supuesto, para cualquier lector-a del blog aunque no haya asistido a ninguna charla.

Puedes escribir tu pregunta en los comentarios, al final de este texto

-----------

La primera cuestión:

"Hola. No me ha quedado claro por qué desde las calles del ensanche de Bilbao podrá verse el Sol totalmente eclipsado"

Normalmente será difícil ver el Sol en el momento del eclipse total desde zonas urbanas porque la altura será pequeña (de apenas 8º en el País Vasco) y en la mayoría de los casos los edificios contiguos lo taparán. Pero casualmente la Gran Vía y las calles paralelas a ella, a ambos lados (al menos 6) están orientadas a 15º desde el Oeste hacia el Noroeste, aproximadamente hacia la posición del Sol en ese momento por lo que además de tener el horizonte lejano se verá el Sol en el fondo de la calle sin obstáculos.

En este mapa las zonas en que podrá verse están en color blanco y las sombras en gris:

Mapa obtenido con https://shademap.app
Con ese mismo simulador, puede comprobarse que Bilbao es la única capital de las 21 en que se verá eclipse total, en que ocurre algo similar.

------------------

"En la charla en la Uni de hoy has comentado que el mapa del eclipse publicado por el departamento de Ciencia y Universidades no te parecía adecuado. Pero dado su aspecto no parece algo práctico, sino una especie de icono para la campaña, donde pueden disculparse licencias o pequeñas inexactitudes"

De acuerdo. Si es solo un logo se puede simplificar, pero no cometer errores tan burdos y sencillos de solucionar con solo fijarse un poco.

De las tres provincias, Alava es la única en que el eclipse es total en todo su territorio, y sin embargo en este “logo” dejan fuera parte de esta provincia. Lo mismo ocurre con parte de Gipuzkoa. Nada más verlo, un habitante de Asparrena, de Oñati, de Arrasate, de Eskoriatza, … se desilusionará viendo claramente que desde allí no podrán ver la noche en pleno día. Cuando la realidad es que sí.

En el mapa de la derecha (contrastado y correcto), la línea amarilla delimita la zona desde donde se verá el eclipse total y el parcial.
Se ha marcado con flechas azules la zona nordeste de Álava, donde la diferencia entre los dos mapas es muy evidente

¿Tan difícil era corregirlo? ¿Ningún responsable se ha dado cuenta? Como he dicho en la charla, todos nos equivocamos alguna vez, pero… ¿no había nadie del equipo que viera tan claro error?

De una manera sencillísima se puede corregir. 

Por otra parte, el dividir en 2 zonas diferentes el territorio donde se ve el eclipse total (en 3 zonas incluida la zona del parcial), ¿De quién ha sido la gracia? No tiene ningún sentido. En ninguna parte se ha hecho tal distinción en ningún eclipse. Hay 2 zonas: donde se ve el eclipse total y donde no se ve. Porque a todos los efectos didácticos y emotivos el verlo 20 segundos de totalidad o verlo un minuto y medio no hay diferencia.

¿Es solo por estética de utilizar 3 colorines?

Si se quiere ser meticuloso y didáctico, se pueden hacer líneas por ejemplo cada 5 minutos, como se ha hecho en algún lugar, pero no una primera y una segunda división, que es lo que parece que se quiere mostrar aquí. A quien se le ha ocurrido se le podía bajar a regional, para que diferencie bien las regiones

Perdón por el tono, pero cada vez que veo ese mapa en un interesante proyecto didáctico para toda Euskadi…

--------------

Bueno, pero las famosas gafas hay que utilizarlas en todo momento en que estemos mirando el Sol?

En principio, si. Hay que proteger la vista con las gafas siempre que mires al Sol. Durante la totalidad debes quitártelas y mirar directamente para apreciar el Sol negro, la corona solar, y el paisaje oscurecido. Solamente podrías seguir sin ellas un instante cuando acabe la totalidad para apreciar el anillo de diamantes o las perlas de Bailey, aunque son episodios muy breves  que pueden captarse mejor por métodos fotográficos.

A veces ocurre que cuando hay bruma o nubes no muy densas no se ve nada con las gafas, pero seguro que alguna vez (con eclipse o sin él) has visto el Sol sin problema. Lo podrías hacer también si ocurre esto en el eclipse, pero en un intervalo muy breve.

También hay que decir que no vas a tener las gafas puestas durante las casi dos horas, porque resultaría muy aburrido. Dicen que lo habitual puede ser mirar unos 10 o 20 segundos, luego comentas o charlas con los vecinos de observación y un rato después volver a mirar. Teniendo esto en cuenta las gafas se pueden compartir entre varias personas.

-------

¿Por qué en Italia o Túnez no podrán ver el eclipse? Lo comentaste pero creo que no lo entendí.
Gracias y un saludo

Este es el mapa del eclipse:

Tal como se ve en este mapa, la línea gris oscura que marca la totalidad comienza en una zona de Siberia y acaba poco después de Baleares. En ese punto del Mediterráneo el Sol totalmente eclipsado se pone por el horizonte. Más al este, por ejemplo en los dos países que mencionas, verán comenzar el eclipse que será parcial ya con el Sol cerca del horizonte poco antes de ponerse, y justo cuando faltaría poco para la totalidad se pone y no pueden verlo. Mala suerte.

Lo contrario ocurre en Siberia, antes de la línea de la totalidad. Desde allí, por la mañana se vería solo una parte del final del eclipse porque  el Sol saldrá una vez que ha acabado la totalidad.

¿Nos impedirán los montes ver el eclipse?

 

Todavía faltan casi 4 meses para “nuestro eclipse” pero por todas partes se hacen referencias al mismo, a cómo será el fenómeno, a los mejores lugares para observarlo o a lo difícil que resulta ya encontrar un alojamiento para esa fecha en la franja de la totalidad…

Uno de los problemas de cara a su observación surge porque el fenómeno ocurrirá hacia el final de la tarde y si no calculamos bien el lugar desde el que lo pensamos observar, podría ocurrir que tuviéramos el Sol ya debajo del horizonte en el momento clave de la totalidad.

Puede que las nubes no sean el mayor obstáculo para ver el eclipse si no hemos calculado el lugar en que estará el Sol

Es cierto que en toda la franja de totalidad de la península y Baleares lógicamente el eclipse total acabará antes que la altura del Sol sea cero. Cuanto más hacia el este ocurrirá con el Sol más bajo, y por ejemplo en La Coruña estaría a 12º a las 20:28 el máximo, mientras que en Burgos a 8º18´ a las 20:29, en Valencia a 4º33´ a las 20:33 o en Palma a solo 2º36' a las 20:32.

Además también cuanto más hacia el este la situación es peor porque aparte de que el eclipse ocurre en general más tarde, el Sol se pone antes, aunque también hay pequeñas diferencias por la latitud y la forma alargada de la sombra de la Luna.

En este mapa se puede ver la altura del Sol durante el eclipse total en cada capital de provincia de la franja. Lógicamente cuanto mayor sea esa altura más fácil será encontrar un lugar desde el que se pueda observar sin obstáculos.

Aunque en todos los lugares de la franja podría verse el eclipse con un horizonte plano de altura cero, la orografía de la zona donde estemos o incluso los edificios nos podrían jugar una mala pasada, que vamos a intentar solucionar:

El día simétrico

Se ha difundido un método para conocer con antelación la posición del Sol en el momento del máximo del eclipse (o de todo el fenómeno completo). Se trata de observar la situación el 30 de abril o días contiguos a la misma hora (luego concreto un poco más) del final de la totalidad del eclipse, porque ahí estará también el Sol en el momento clave.

El motivo es que el 30-4 (en algunos lugares se dice el 29 o incluso el 28) y el 12-8 son simétricos respecto al 21 de Junio día del solsticio (52 días antes y después del mismo), y las trayectorias del Sol serán prácticamente iguales. Ahora cada día el Sol traza una trayectoria más alta, hasta el 21 de junio en que se invertirá la situación y se llegará a la misma posición.

Es curioso que en muchos de los artículos o conferencias sobre el tema se cita erróneamente el día 28, cuando deben transcurrir 54 días hasta el solsticio en vez de los 52. La diferencia se aprecia también con un simulador.

Sin embargo, aunque aproximadamente pueda valer para saber dónde estará el Sol en el momento del máximo, este método no es exacto porque las posiciones coincidirán a la misma hora, pero hora solar, y entre ambas fechas hay una diferencia de 8 minutos por la ecuación del tiempo. Si por ejemplo en nuestra localidad la fase total del eclipse acaba a las 20:30, tendríamos que mirar el día 30 de abril cuando nuestro reloj marque las 20:22 , porque a las 20:30 estará más de un grado más bajo.

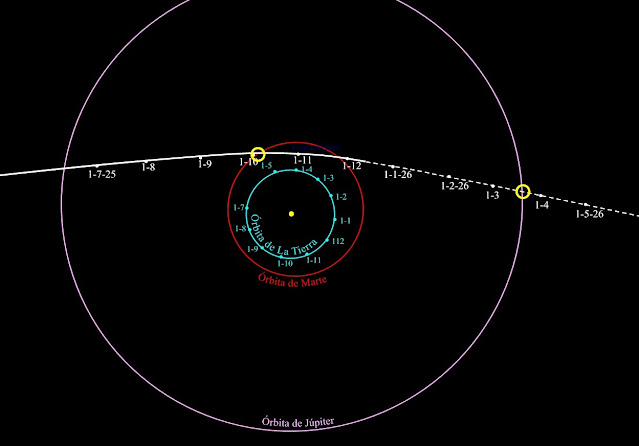
Cuando estará a la misma altura y a la misma hora que el día del eclipse será el 5 de mayo, aunque se situará más de 2 grados hacia el Noroeste como se aprecia en este gráfico: 

Se ha representado la situación en Valencia (la altura sobre el horizonte respecto a la separación de las diferentes trayectorias), por ser una de las capitales con mayor dificultad para averiguar si el horizonte obstaculiza la observación, pero las demás serán análogas

En este gráfico se aprecia que la observación el día 30 de abril (o el 29 o el 28) únicamente nos proporciona el itinerario aproximado que seguirá el Sol el día del eclipse, pero eso no nos permite saber si salvará el horizonte real o no. 

Por ejemplo, el día 30 a la hora del eclipse (20:33:24) en el caso que recoge el gráfico da una posición para el Sol por debajo del horizonte real, pero el día del eclipse a esa misma hora estaría por encima y se vería sin problema.

Como se ha dicho, todo esto es debido a la ecuación del tiempo, que produce una discrepancia variable entre la hora solar y la hora media, y puede parecer que juega a nuestro favor en el sentido de que nos dará un margen de seguridad, ya que si miramos la situación el día 30 a la misma hora y vemos el Sol, el día del eclipse estará más alto y no tendremos problema, pero no será el lugar correcto, además de dejarnos con la duda si en ese momento se ha ocultado.

Bueno, en realidad puede decirse que los resultados obtenidos el 30-4 o el 5-5 pueden ser análogos: el primero nos daría la componente horizontal (el azimut) del Sol el día del eclipse y el segundo la altura. Está claro que el segundo puede ser más clarificador porque el horizonte más frecuentemente es horizontal, pero podría haber algún caso en que en la zona sea muy irregular, pero con ambos datos de la horizontal y la altura ya tendremos el punto exacto. 

De todas formas quizás la mejor solución sea tomar la posición del Sol el día 30 de abril, pero 8 minutos antes de la hora del final del eclipse.

En cualquier caso debemos conocer esa hora en que se producirá el eclipse. De nada nos sirve conocer la trayectoria del Sol si no conocemos la hora. La variación de un lugar a otro no es muy grande (menos de 5 minutos de Galicia a las Baleares), pero si queremos ser más precisos podemos tomar el dato de el siguiente mapa que nos da el momento de finalización de la totalidad.

Hora en que acaba la fase total del eclipse en las diferentes capitales de provincia y delimitaciones por cada minuto para estimarlo aproximadamente en otros lugares

La extraña forma de las líneas que delimitan los minutos se debe a que la sombra de la luna al final del eclipse, lejos de ser circular, es similar a una elipse muy alargada.

Pero se han escrito (incluso de fuentes generalmente bien informadas) textos como:

 "

Sobre la fecha, ya he dicho que no es el 28 sino mañana día 30  y es curioso la cantidad de noticias que decían el 28. Ya hasta se puede pensar mal porque la semana pasada en la mayoría de los lugares se decía el 28 y luego ya el 30.

Pero ¿Por qué entre las 7 y las 9? Con hacerlo entre las 8:15 y 8:25 es más que suficiente. Si en ese momento el Sol se ha ocultado detrás de un monte, edificio o árboles, no se verá el eclipse desde ahí. En caso contrario casi seguro que si, pero hay que afinar según los cálculos que se explican luego. Si en ese intervalo está lejos de los posibles obstáculos, se verá también en 12 de agosto.

¿Qué significa que el horizonte esté limpio y el Sol se vea sin interferencias? ¿Cuándo? porque en algún momento antes de las 9 tiene que ponerse.

Resumiendo: Mira en el mapa, (o haz una estimación) de la hora en que termina el eclipse en tu localidad y réstalo 8 minutos. Si a esa hora ves el Sol el 30 de abril (o días contiguos) también lo verás cuando esté eclipsado el 12 de Agosto. 

Y si estos días está nublado, tienes otro método aunque no tan directo. Puedes obtener una simulación  de la situación en https://shademap.app que te proporciona las sombras a cualquier hora. Lógicamente desde la zona sombreada no se verá el Sol.

increíbles situaciones para empezar la semana

 

Si anteayer publicaba un post con “bonitas imágenes para acabar un fin de semana” es obligado escribir otro con “increíbles situaciones al comienzo de la semana” No solo porque después de un finde hacen falta ganas y motivación para empezar de nuevo, sino también para hacer justicia ya que lo anterior se podía observar mejor desde el hemisferio norte mientras que esto es exclusivo del hemisferio sur.

Además todo cuadra porque aquello anterior era para el comienzo de la noche, sobre todo la del domingo y esto será para la madrugada, fundamentalmente del lunes: ¡A levantarse con ganas que el cielo está animado!

Entre las dos situaciones están implicados todos los planetas: Si en el primero se hablaba de Venus, Júpiter y Urano, en este caso se producirá una cerradísima conjunción de Mercurio, Marte y Saturno (no recuerdo haber visto nunca nada igual), mientras que Neptuno está por la cercanía.

El comienzo de la semana será extraordinario de madrugada: tres planetas se verán totalmente alineados y enormemente cercanos (de Mercurio a Saturno solo medio grado y de Saturno a Marte apenas 1º). Neptuno (el último planeta que falta entre las situaciones recogidas en los dos post) no se ve sin telescopio pero no se halla muy lejano a este trío.      

Hay que decir que las ilustraciones del post anterior eran fotos (algunas con añadidos), y en este caso deben ser dibujos, que mi cámara no llega al hemisferio sur.

Desde Buenos Aires, una hora antes de la salida del Sol

No es que haya hecho un gráfico ridículamente pequeño (que 10º es muy poco), sino que no tendría sentido representar los planetas más separados, porque no lo están.

La imagen del martes será ligeramente diferente y la línea recta entre los 3 planetas se transforma en un triángulo casi equilátero 

Desde Buenos Aires, una hora antes de la salida del Sol

Unos días antes, concretamente el miércoles 15, aunque los 3 planetas más destacados no estaban tan próximos entre sí, la imagen fue interesante porque pasó por allí la fina luna menguante a falta solo de 2 días para nueva, y Neptuno se situaba entre los otros planetas.

Montón de astros juntos 

Esta situación es prácticamente imposible de apreciar desde el hemisferio norte porque la elongación de los planetas (la distancia angular desde el Sol) es relativamente pequeña y en primavera de madrugada la eclíptica está muy poco inclinada de manera que salen poco antes que el Sol en un cielo ya muy brillante.

Ahora he representado los planetas solo media hora antes de salir el Sol. En esos momentos el cielo estará tan brillante que será imposible distinguirlos. Una hora antes, quizás el cielo estaría suficientemente oscuro, pero los planetas estarían aún bajo el horizonte.

En el hemisferio sur que es otoño, ocurre lo contrario con la eclíptica al amanecer, que está más vertical, como expliqué en este post y allí todo es favorable a pesar de que las declinaciones de Marte, Mercurio y Saturno son Norte.

Para comparar la inclinación de la eclíptica voy a poner esa situación desde Buenos Aires y aprovechando para añadir un dato más con las posiciones antes de la alineción, utilizo la fecha del domingo por la mañana, por si vives en el sur y, aunque no sea lo habitual, casualmente te toca madrugar para ir a trabajar.

La eclíptica estará casi vertical

La situación del domingo al principio de la noche que es favorable desde el hemisferio Norte, no es tan difícil en el Sur porque la elongación (la de Venus que es la menor de los astros que se citaban en el post anterior) no es tan pequeña y su brillo es mucho mayor que el de Mercurio, Marte o Saturno. Incluso una hora después de la puesta de Sol en Buenos Aires, Venus y la Luna estarán sobre el horizonte aunque a baja altura pero su brillo permitirá distinguirlas, lo que probablemente no ocurrirá con las Pléyades.

La Luna ya se habrá separado de las Pléyades porque han pasado unas horas desde que se vieron en Europa

Que la madrugada te sea provechosa.

Bonitas imágenes para acabar un fin de semana

El cielo nos ofrece frecuentemente espectáculos diversos: desde los eclipses, ocultaciones, conjunción de planetas, presencia de algún cometa brillante, lluvias de meteoros, …

Lo de este próximo domingo día 19 de abril no es uno de esos fenómenos espectaculares, sino algo que podría pasar desapercibido si no nos fijamos bien: la presencia de varios astros de diferente tipo en una reducida zona del cielo: 2 planetas (de brillo muy diferente), la Luna, el cúmulo de las Pléyades,… Algo que no estará tan anunciado pero será más variado y quizás más atractivo.

El día 19 Luna de 2 días junto a las Pléyades, mientras Venus se sitúa cerca y por allí anda también Urano (señalado con una flecha). A la izquierda de la imagen aparece la estrella Aldebarán y las Híades.

Y algo más apartado, al oeste de esa zona, que llamará más la atención y que lleva ya bastante tiempo sorprendiendo a quienes al principio de la noche miran hacia arriba: el planeta Júpiter, muy alto (desde  una latitud media Norte) y extraordinariamente brillante, que todavía estará cercano a las espectaculares constelaciones de invierno que ya nos van diciendo adiós.

Júpiter en todo lo alto, y entre los árboles la constelación de Orión y las brillantes estrellas Proción y Sirio. A la derecha, parcialmente tapado por el árbol, el cúmulo de las Híades con Aldebarán, donde comenzaría la imagen anterior.

Es curioso, que aunque el brillo de Venus es siempre mayor que el de Júpiter, ahora debido a su baja altura (y sobre todo si hay algo de bruma por el horizonte) es el quinto planeta el que más destaca y el que se lleva la mayoría de las miradas.

Y todo esto aderezado con la lluvia de meteoros de las líridas que pueden verse entre el 16 y el 26 de abril pero ya podría aparecer alguna de ellas. La fase lunar el día del máximo (el 22) seguirá siendo fina y se pondrá pronto, con lo que no molestará con su luz y las condiciones serán favorables para la observación.

Una lírida por el Sur de Orión, capturada por Aleksandar Pasaric

Volviendo al principio, el domingo 19 podremos ver a la fina luna junto al cúmulo de las Pléyades, y tal como se recogió en este post esto ocurre todos los meses desde 2024 hasta 2029 aunque con diferente fase y desde distinto lugar. En este caso la fina fase de la Luna podría hacerlo más atractivo, aunque la mejor imagen se verá desde una zona de Siberia en que la Luna aparece rodeada (como incrustada) entre 8 o 9 de las estrellas del cúmulo. 

Preciosa ocultación desde Vorkuta (Siberia) 65º N  67º E, donde en un determinado momento la Luna quedará rodeada o "encerrada" entre 8 de las estrellas más brillantes de las Pléyades, Similar a lo que se vio en Madrid el 1-4-25 , pero en aquella ocasión con una fase menos fotogénica.

Desde la península Ibérica la Luna oculta a un par de estrellas brillantes del cúmulo pero será de día, sobre las 19:30, y aunque en otras circunstancias con un telescopio se podría intentar su observación, la cercanía del Sol lo hace prácticamente imposible.

Siempre es atractivo cuando algún objeto celeste se sitúa en la zona entre Pléyades e Híades porque hace destacar la belleza de éstas, y no es muy infrecuente por estar cerca de la eclíptica.

Así, Los siguientes días, sin ser tan destacadas, se producirán otras circunstancias que no dejan de tener su interés

22-4 La Luna junto a Júpiter en el centro de la constelación de Géminis

En 3 días la Luna se mueve de las Pléyades a Géminis, engorda un poco y se sitúa junto a Júpiter que apenas se movió

23-4 Venus junto a Urano en Tauro, cerca de las pléyades

En este caso es Venus prácticamente el único que se ha movido sobre el fondo estrellado

Aparte de la Luna, está claro que Venus y Júpiter van a ser los animadores del principio de la noche en estos meses.

En esta imagen (de muy mala calidad por las condiciones del cielo y donde se han ampliado los dos en la misma medida) se puede comparar como se veían ambos planetas el día 10. Ahora mismo (y más el día 19) Venus habrá ganado mucho en brillo y altura. ¿suficiente como para competir con Júpiter?

Aquí Venus apenas se distingue pero en la siguiente foto, ya avanzado el crepúsculo y a pesar de la contaminación lumínica, se aprecia claramente.

Bien es cierto que, si las condiciones del cielo son buenas, el segundo planeta destacará como ningún otro al final del crepúsculo, bastante más que Júpiter. Ambos se van aproximando vistos desde la Tierra y a primeros de junio tendrán su conjunción y, uno junto al otro, quedará claro quien domina en brillo.

Actualización 17-4

Efectivamente, ayer mismo con unas condiciones mejores del cielo, Venus (en la zona inferior derecha) y Júpiter (arriba a la izquierda) aparecían dominando claramente el crepúsculo vespertino.

Si en la tediosa tarde del domingo hay claros en el cielo intenta ver a estos dos planetas, a la fina Luna y todo lo demás que darán ánimos para olvidar que se acaba el finde.

Actualización 20-4

Aunque tuvimos algunas nubes, Íñigo Loit Larrañaga consiguió esta bonita imagen de la conjunción de las pléyades con la Luna en la que se aprecia muy bien su luz cenicienta.

Yo tuve el cielo más cubierto, pero en algún momento pudieron verse Venus (en la parte inferior de la imagen) y la Luna:

La Luna y las plantas. La influencia de la Luna (5)

 

Hace ya tiempo que escribí una serie de cuatro artículos sobre la influencia de la Luna, y aunque prometí un quinto capítulo orientado a las labores agrícolas, se quedó en el olvido (mejor dicho encerrado en su carpeta) y voy a intentar continuar ahora.

Bueno, el motivo de no publicarlo fue el temor de que fuera rechazado por muchos lectores que creen a pies juntillas en los "poderes de la Luna en los cultivos" y dejaran de leer este blog, circunstancia que ya me ha afectado en más de una ocasión en otros ámbitos como cuento al final.

¿Influye la Luna en las plantas?

Pero he decidido completar el tema y, haciendo un resumen, en los 3 primeros capítulos se detalló el tema de las mareas, algo evidente y científicamente demostrado, pero que sirvieron de preámbulo al cuarto en el que se ponía en duda (o más bien se demostraba su falsedad) casi la totalidad de la supuesta influencia de nuestro satélite sobre las personas.

La Luna no nos influye a los humanos (al menos en todo lo que se ha podido estudiar), aunque hace millones de años fuera decisiva para el surgimiento de nuestra especie

Como he dicho, ahora llega el turno de las plantas. Quizás en este campo se den la mayor parte de las creencias de la influencia lunar, y parece que siempre se ha mirado la Luna antes de podar, plantar o recolectar. ¿O quizás no?

En este ámbito también yo antes me creía todo lo que oía: “Si lo dicen los agricultores, ellos sabrán sobre las faenas del campo que es su trabajo”. Pero después de la experiencia que cité en el tema anterior, realizada con ayuda de mi alumnado, y que demostraba la falsedad de la creencia del aumento de los nacimientos en luna llena que algunos médicos afirmaban, ya dudo de casi todo lo que oigo.

Ahora me inclino por pensar que todas esas normas “el…hay que recogerlo en menguante, pero cuidado con podar las…en creciente” han sido muy útiles de cara a establecer un calendario de trabajo. Guían a muchas personas que sin ellas serían desorganizadas, asignan una tarea, pero no tienen fundamento.

Porque hay varias razones para pensar que tampoco en la agricultura influye la fase lunar, que es posiblemente el objeto de la mayor parte de esas creencias y supersticiones, y seguramente las más aceptadas aunque no es difícil comprobar que no tienen sentido. Comenzando por un razonamiento que ya surgió, como consecuencia de la atracción gravitatoria, en este caso sobre la savia de las plantas: “Que no hay que podar cuando la savia está arriba, porque la planta se desangrará. Y que estará arriba cuando la Luna atraiga con más fuerza, es decir en luna llena”.

Este razonamiento se cae por su peso porque la Luna llena de día (que es cuando se hacen prácticamente siempre las labores de poda) se sitúa bajo el suelo, y no arriba. Otros dicen no podar en creciente, pero tampoco:

“La mejor luna para podar plantas es la luna menguante ya que la savia desciende hacia las raíces, lo que reduce el «sangrado», acelera la cicatrización de las heridas y previene enfermedades. Es ideal para podas de mantenimiento y formación. En cambio, para estimular el crecimiento tras la poda, se recomienda la luna creciente”.

Estas frases son una inocente y errónea interpretación de los términos CRECIENTE (parece que indica hacia arriba) y MENGUANTE (hacia abajo). Pero unos mínimos conocimientos astronómicos nos dicen que la luna menguante por la mañana está por encima del horizonte, y por ello si influyese su atracción gravitatoria no haría descender la savia hacia las raíces, sino todo lo contrario. 

Aunque las palabras “menguante” o “creciente” pudieran indicar circunstancias contrarias, es totalmente absurdo porque tanto la marea en una y otra fase son iguales y de poca intensidad. La iluminación es igual y lo único que cambia son las horas en que puede verse sobre el horizonte, pero ni siquiera el número de horas.

Además una luna menguante la veremos ascender respecto al horizonte durante la mayor parte de las horas.

Por otra parte, suponiendo que en algún momento la savia descendiese o ascendiese por el interior de la planta debido a la atracción lunar, los científicos han calculado cuánto sería, y el resultado es sorprendente: menos del tamaño de un átomo. O sea, nada.

¿Y por qué sube y baja el agua del mar? Porque la masa de ese agua es infinitamente mayor que la de la savia de cualquier planta. Ese factor interviene en el cálculo y es decisivo.

Los periodos de la supuesta influencia en la plantas y los de las mareas son totalmente distintos. Por ejemplo en 24 horas la fase lunar apenas cambia muy ligeramente, por lo que en cada fecha estaría indicado podar o no podar. Pero las mareas suben y bajan continuamente, habiendo cada 24 horas dos mareas altas y dos mareas bajas. También con luna nueva (que suponen que la savia baja), hay dos mareas altas, y es una de las fases en que se producen mareas vivas al ser la atracción gravitatoria más eficiente.

Ciclos de mareas durante 24 horas

Aunque sea en broma, habría que decir: ¡Cuidado! Si quieres que la savia de tus plantas vaya a las raíces, no te vale con podarlas en luna nueva. Mira la hora y la tabla de mareas.

Siendo rigurosos en los estudios, hay que decir que es difícil comprobar si la Luna afecta a las plantas (si es que les afecta algo) porque hay otros factores (humedad, temperatura) que está claro que las afectan mucho más, que son muy variables y no tienen periodos fijos.

Dos experimentos

En este ámbito es muy difícil hacer estudios, y seguro que no serían demasiado fiables. Aún suponiendo que la Luna pudiera afectar a los cultivos, la meteorología lo haría en mucha mayor medida, de manera que sería difícil sacar conclusiones y separar una causa de la otra. Pero este mismo razonamiento implica que todas estas creencias no tengan una base fundada. 

En cualquier caso, algo se ha hecho y cito dos casos que me han llegado de primera mano:

- Bajo la dirección de un reconocido profesor de la Universidad Politécnica de Cataluña a quien conozco personalmente, se realizó un experimento para contrastar la creencia en aquellas comarcas de que los ajos picaban más si se recolectaban en determinada fase lunar. Los resultados fueron negativos y totalmente concluyentes.

- En un informativo de la televisión vasca EITB se anunciaba en los titulares que había sido probada la influencia en la fase lunar en un prestigioso centro de formación profesional de Gipuzkoa. Pero los resultados que aparecían en las imágenes de troncos de madera cortados en distintas fases lunares no eran en absoluto concluyentes.

Conocido el tema, contacté con la responsable de la experiencia, le pedí los resultados concretos y en un primer momento no puso ninguna objeción: “Que ya me los mandaría” Luego se lo pensó mejor y “que prefería llevármelos personalmente”. Pensé que querría comentar conmigo algunos detalles, pero canceló la visita un par de veces con diversas escusas. Finalmente le dije que ya iba yo a su centro de trabajo, dijo que vale, que ya me diría. De eso… hace 7 años y todavía estoy esperando que me diga cuándo me recibirá.

Evidentemente si el experimento es positivo estarían satisfechos de que se difundiera y su actitud sería muy diferente.

Aunque algo salió en la tele, yo me quedé sin saber cual era el bueno y en que fase lunar se había cortado (estas imágenes son figuradas, ya que no llegué a verlas)

Agricultura biodinámica

Aunque hay que decir que estas creencias siempre han tenido muchos seguidores entre los agricultores, han recibido un palo enorme desde el mismo sector, con las propuestas de Rudolf Steiner (1961-2025) con lo que llamó agricultura biodinámica, porque utiliza también la Luna pero con criterios muy diferentes a los tradicionales. Como otras teorías modernas ha encontrado muchos seguidores, y se han escrito más tratados sobre agricultura biodinámica que sobre todos los conocimientos populares de siempre. Todos los años se editan extensos manuales, con las instrucciones para plantar o recoger diversos cultivos, que tienen un gran éxito en las librerías.

3 ejemplos de estas publicaciones. Sobre todo la de la derecha trae una cantidad enorme de datos y es la más conocida y vendida con gran éxito en librerías

El asunto clave es que la agricultura biodinámica utiliza también la Luna, pero no sus fases sino su situación ascendente o descendente, que no tiene nada que ver y en ocasiones da criterios opuestos a las fases.

Un cuarto creciente puede coincidir con la luna ascendente un mes, pero otro mes con la descendente. Por ejemplo según la tradición deberíamos plantar las cebollas en la primera semana de abril de un determinado año, cuando según los biodinámicos estaría totalmente desaconsejado.

Una página del manual mencionado antes. Leyéndolo e interpretándolo podría pasarse el tiempo de realizar la tarea agrícola.

Rudolf Steiner, con sus lunas ascendentes y descendentes se ha cargado todo el saber popular y nos ha dado la razón a quienes decíamos que la fase lunar no puede influir en las plantas.

Pero además lo suyo es un invento moderno sin base científica y difícil de llevar a cabo si no compramos uno de esos libros porque todo se hace complicado. Para averiguar si hoy la Luna es ascendente o descendente no basta con mirarla, como sería para comprobar su fase, sino que habría que haber hecho observaciones los días anteriores, comprobar si a una misma hora está más alta o más baja y aún así será difícil si no hacemos fotografías. Y los agricultores de siglos pasados no tenían cámaras. O sea, que este criterio no es anterior a 1970, cuando lo inventó Steiner.

En el gráfico la luna del día 21 sería ascendente porque está más alta que la del 20.
Incluso la nomenclatura que utiliza esta publicación en euskera (ilgora e ilbehera) para referirse a ascendente y descendente contradice el significado correcto de estos términos (creciente y decreciente)

Las afirmaciones de Steiner no se quedan en este aspecto de la Luna, sino también utiliza la distancia a la Tierra, la posición respecto a los nodos, además de considerar las posiciones de los planetas y las constelaciones. Un galimatías difícil de aplicar. Algunas de sus indicaciones, como “el periodo ideal de eliminar los ratones según las posiciones de los astros”, son de auténtica risa.

Unos criterios inventados por quien fue un oculista austriaco, educador, autor teatral, pensador social, arquitecto, esoterista y autodenominado clarividente (según Wikipedia).

Rudolf Steiner

Pero muchos han hecho dinero gracias a él: Como he dicho, se han escrito muchos más libros que los relativos a las creencia tradicionales, algunos de los cuales sacan ediciones cada año y está claro que ni una ni otra son verídicas porque si una lo fuera, habría desaparecido ya la otra al comparar cosechas guiadas por una u otra.

Bueno, pero “Se dice que las creencias tradicionales siempre llevan algo de verdad ¿no?” Pues a ver como congeniamos “A quien madruga Dios le ayuda” con “No por mucho madrugar amanece más temprano”, o “A la tercera va la vencida” con “No hay dos sin tres” o la que se refiere al tema de hoy “Hombre lunero no hace granero” Que indica que el saber popular tampoco se fía de la Luna.

Es posible, estimado lector, que no estés de acuerdo con el contenido de este post. Me lo puedes decir tranquilamente en un comentario, pero te pediría que por este motivo no dejes de leer el blog. Me ha ocurrido con dos asociaciones que anualmente me pedían que les diera alguna charla sobre los astros y después de que les contara esta historia no volvieron a llamarme.